Changyu Deng | Optimizing battery electrode morphology

This project challenges the current uniform electrode and hopes to develop a tool to find the optimal electrode morphology without any prior assumption on its pattern. Similar problems have been studied in topology optimization which is commonly used in solid mechanics. However, most of them are linear problems where the gradients can be easily derived. For batteries, by constrast, no gradient can be analytical obtained. As a result, current optimization algorithms cannot be used, and we designed a topology optimization algoritm called Self-directed Online Learning Optimization (SOLO). The algoritm was much faster than state-of-the-art gradient-free optimizers, and could be used to optimize electrode geometry.

Background

Since the invention of lithium-ion batteries, porous electrodes have been manufactured in essentially the same way: granulating active materials into powder, mixing them with some additives such as carbon black and binder, and pasting them on conductive substrate. Optimizations have been focusing on tuning parameters such as particle sizes, porosity and electrode thickness, with the assumption of a uniform electrode. Some recent work demonstrated better cell performance by engineering the shape of the electrode with features such as nano cylinders, tunnels and fractal branches. 3D printing has been used to fabricate the structure of batter electrode. On the simulation side, however, there have been few reports on freeform electrode shape optimization. Most shape optimizations assume a particular electrode pattern with a few adjustable dimensional parameters. Therefore, we want to propose a method to optimize porosity distribution of electrode without a prior assumption of the pattern.

Results

We first introduce topology optimization by a fluid-structure optimization example, and then look into the electrode optimization.

A fluid-structure example

We use an example to explain what topology optimization is. As shown in subfigure a below, the fluid enters the left inlet at a given velocity perpendicular to the inlet, and flows through the channel bounded by walls to the outlet where the pressure is set as zero. In the \(40\times 16\) mesh, we add solid blocks to change the flow field to minimize the friction loss when the fluid flows through the channel. Namely, we want to minimize the normalized inlet pressure

\[\min\limits_{\rho\in\{0,1\}^N } \widetilde{P}(\rho)={P(\rho)}/{P(\rho_O)},\]

where \(\rho\) is a 640-dimentional vector with each component equal to 0 (void) or 1 (solid), \(P\) denotes the average inlet pressure, and \(\rho_O=(0,0,...,0)\) indicates no solid in the domain.

Traditionally, this problem will be converted to a continuous problem to solve by a gradient-based solver, since the dimension (i.e., number of variables) is too high for a gradient-free method. Think about all possible cases, it will be \(2^{640}\approx10^{192}\); even if each case needs one second to compute the pressure, it would take \(\sim10^{185}\) years! You cannot get the results before the end of the universe.

Setup and results of a fluid-structure optimization problem with 40x16 design variables. SOLO-G denotes the Greedy SOLO, a variant of our algoritm.

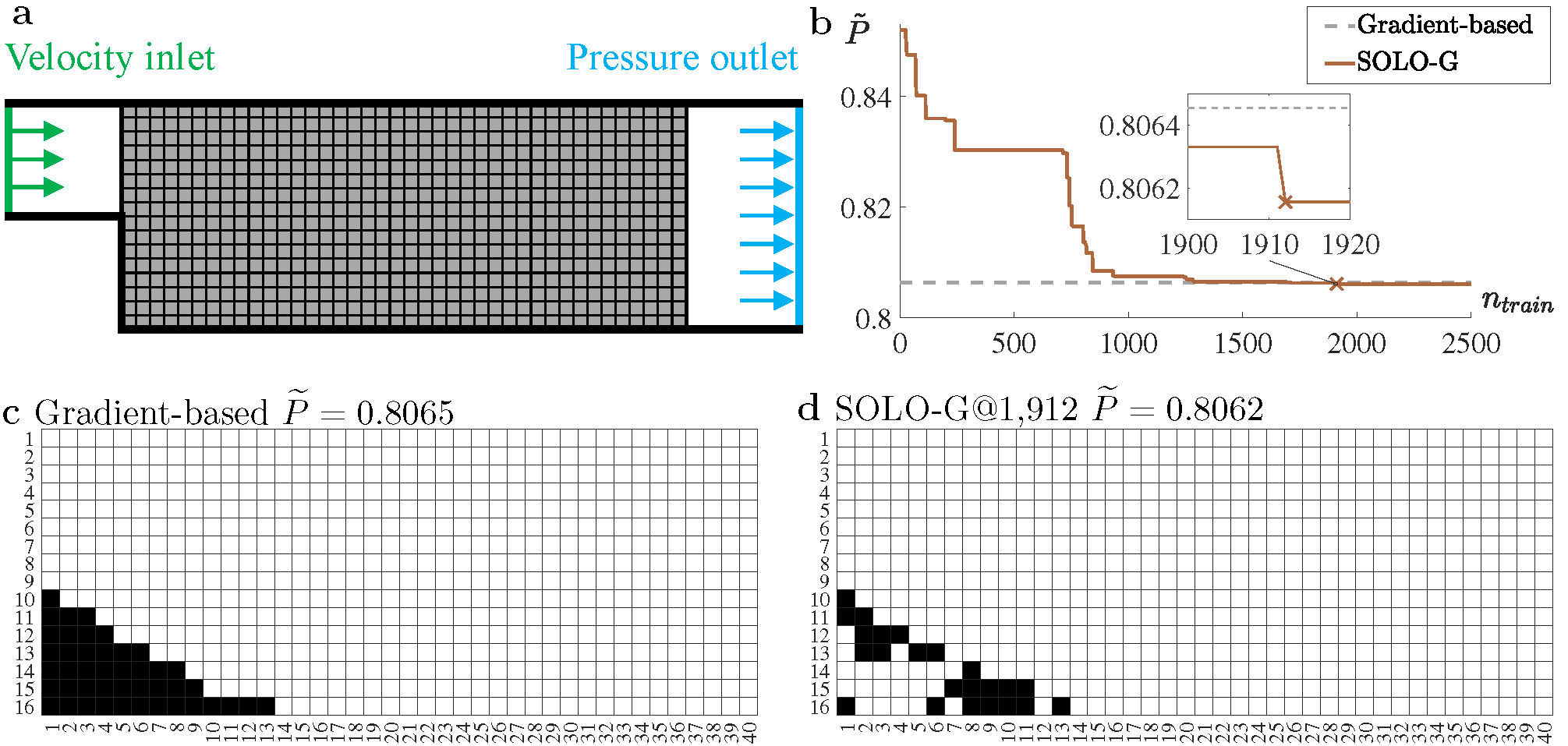
Our algoritm, Self-directed Online Learning Optimiation (SOLO) can significantly boost the gradient-free optimization. Subfigure b shows our pressure curve versus the gradient based (horizontal line). The algoritm only tried 1912 cases to converge (the cross “X”). Our solution (subfigure d) is better than the gradient-based method (subfigure c), since it has a lower pressure.

We just showed a binary example. In fact, we can apply SOLO to continuous problems as well. In our experiments, our algoritm outperforms many state-of-the-art gradient-free algoritms, such as CMA-ES (Covariance Matrix Adaptation Evolution Strategy), BO (Bayesian Optimization), and SA (simulated annealing).

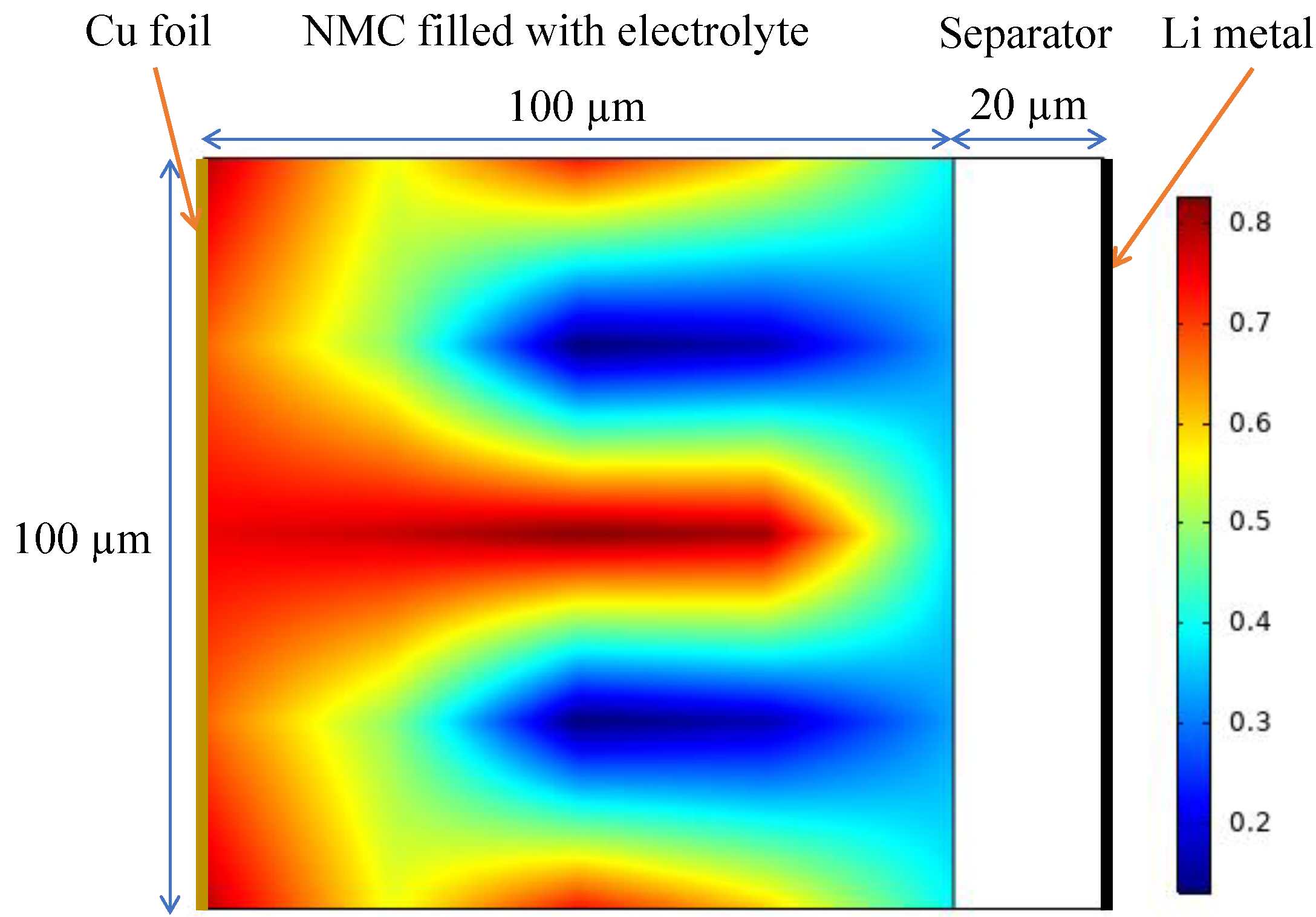
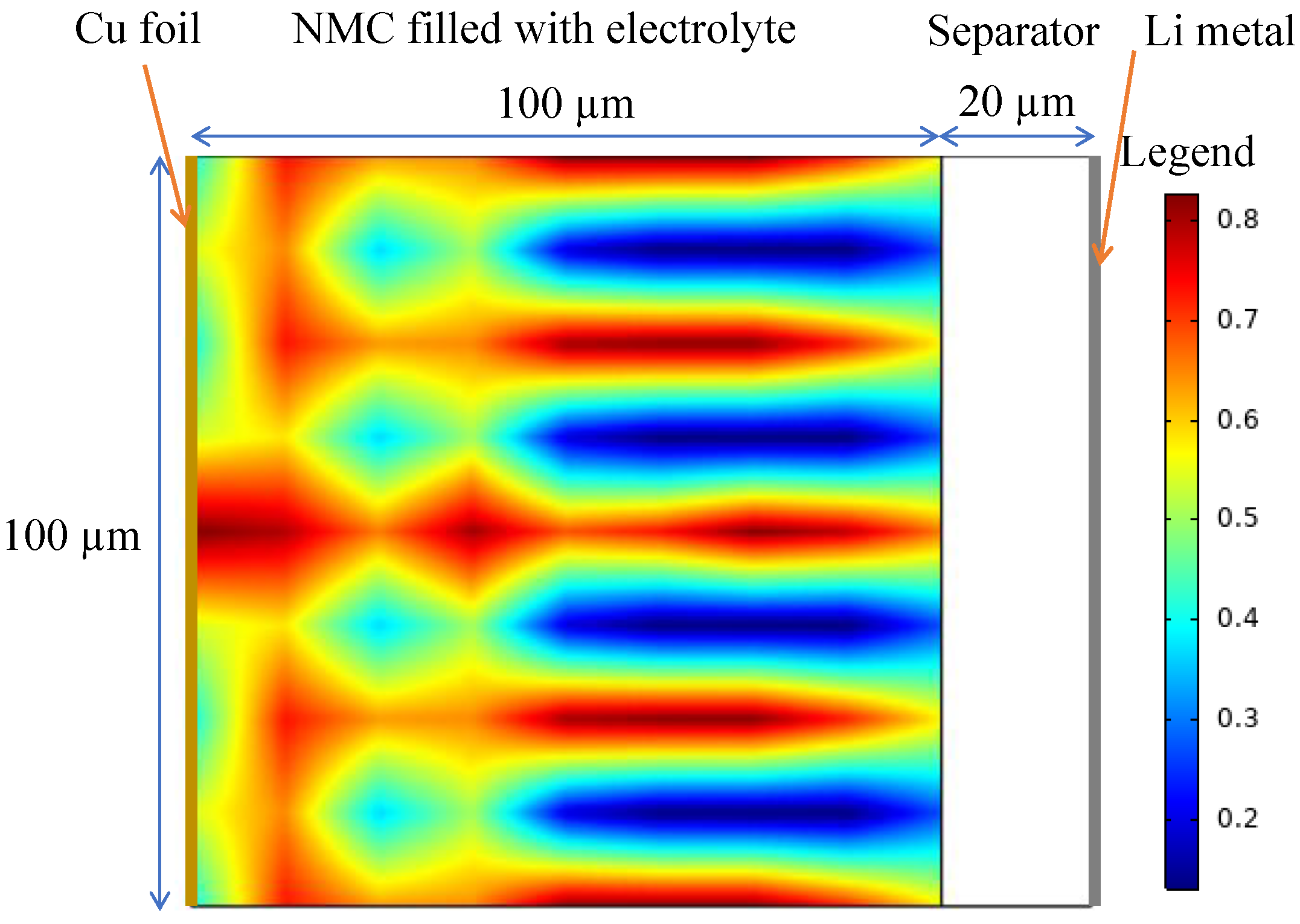
Electrode optimization

We apply SOLO to electrode optimization. Consider a NMC622/Li metal cell, We want to control the solid distribution in a domain to maximize the specific energy density:

\[\begin{array}{c} \underset{\rho=(\rho _1,\rho _2,...,\rho _N)}{\max}E(\rho)\\ \left\{ \begin{array}{l} \sum_{i=1}^N{w_i\rho _i}=0.5\\ \rho _i\in \left[ 0,1 \right] ,\text{ }i=1,...,N\\ \end{array} \right.\\ \end{array}.\]

where \(w_i\) denotes the weight of integration to confine the average volume fraction of solid material to be 0.5. The specific energy \(E\) given a solid distribution \(\rho\) is obtained by discharging the cell from 4.1 V to 3.5 V, calculated by the pseudo three-dimensional model (an extension of pseudo two-dimensional model). The results are shown below.

Optimal solid distribution in a 5x5 mesh

Optimal solid distribution in a 9x9 mesh

A generic battery-cycling optimization framework with learned sampling and early stopping strategies

Changyu Deng, Andrew Kim, and Wei Lu

Patterns 2022

Abs HTML PDF Code

There are many parameters to optimize for a battery, in both simulations and experiments, from design to manufacturing. It is time consuming and costly to evaluate the lifetime performance of batteries since it takes a long period to cycle them. We introduce a generic framework leveraging machine-learning algorithms. The framework is designed to optimize battery parameters to enhance cycling performance in a systematic and efficient way, which allows parallel cyclers, stops unpromising cycles, and automatically yields new configurations of parameters. The framework could reduce the average cycling time per battery from years to months/weeks for cycling experiments or from weeks to days/hours for cycling computations. This method is flexible to scale up for many applications, from fundamental research to industrial development in batteries and other similar fields.
Geometry Optimization of Porous Electrode for Lithium-Ion Batteries

Changyu Deng, and Wei Lu

ECS Transactions 2020

Abs HTML PDF

We report a method to optimize the topology of porous electrodes without a prior assumption of the pattern. We take a two-dimensional NMC-Li cell as an example. The domain of NMC is discretized by a 5×5 mesh and the solid volume fraction is represented by 25 nodal variables. We use a deep-learning-boosted optimization algorithm to find the optimal material distribution that gives the maximum specific energy. The method produces an electrode pattern with 18% higher specific energy than that of a uniform electrode. This generic geometry optimization approach provides a powerful tool for the design and optimization of porous electrodes.
Self-Directed Online Machine Learning for Topology Optimization

Changyu Deng, Yizhou Wang, Can Qin, Yun Fu, and Wei Lu

Nature Communications 2022

Abs HTML PDF Code

Topology optimization by optimally distributing materials in a given domain requires non-gradient optimizers to solve highly complicated problems. However, with hundreds of design variables or more involved, solving such problems would require millions of Finite Element Method (FEM) calculations whose computational cost is huge and impractical. Here we report Self-directed Online Learning Optimization (SOLO) which integrates Deep Neural Network (DNN) with FEM calculations. A DNN learns and substitutes the objective as a function of design variables. A small number of training data is generated dynamically based on the DNN’s prediction of the optimum. The DNN adapts to the new training data and gives better prediction in the region of interest until convergence. The optimum predicted by the DNN is proved to converge to the true global optimum through iterations. Our algorithm was tested by four types of problems including compliance minimization, fluid-structure optimization, heat transfer enhancement and truss optimization. It reduced the computational time by 2 5 orders of magnitude compared with directly using heuristic methods, and outperformed all state-of-the-art algorithms tested in our experiments. This approach enables solving large multi-dimensional optimization problems.

Background

Results

A fluid-structure example

Electrode optimization

Related publications