Diffusivity from EIS and GITT

GITT and EIS are two popular techniques to measure diffusivity. Yet, their results sometimes have up to orders of magnitude difference. This project resolved the discrepancy of diffusivity measurement of these two methods.

Galvanostatic Intermittent Titration Technique (GITT) and Electrochemical Impedance Spectroscopy (EIS) are two popular methods to measure the diffusivity of lithium ions in the electrode particles. What has puzzled the community for a long time is that these two techniques often give an order of magnitude difference in the results. This project aims to resolve the discrepancy.

By analyzing the diffusion profile and approximation error for various particle geometries, we show that these two techniques are consistent only when the current excitation does not impact deep inside the particles, which correspond to the condition of short pulse time for GITT or high frequency for EIS. GITT does not depend on particle size by its assumption while EIS does. Thus we propose an innovative approach of using EIS to determine diffusivity accurately independent of particle size or geometry. We further demonstrate experimentally that the two techniques yield identical results under the right measurement conditions.

Background

To measure the particle diffusivity in li-ion batteries, there are two popular methods, GITT and EIS. As shown in the figure below, GITT gives an direct current pulse, and calculate the diffusivity by

\[D=\frac{4}{\pi}\left(\frac{IV_M}{SF}\right)^2\left[\left(\frac{\mathrm{d\ }U}{\mathrm{d\ }\delta}\right)/\left(\frac{\mathrm{d\ }V}{\mathrm{d\ }\sqrt{t}}\right)\right],\qquad (1)\]

which is determined by the cell voltage response \(\left(\frac{\mathrm{d\ }V}{\mathrm{d\ }\sqrt{t}}\right)\) and other material perperties. EIS gives an alternating current pulse at different frequencies. The diffusivity is obtained by fitting the impedance data to a model, such as the semi-infinite solid diffusion model or the equivalent circuit model.

Schematic of lithium ion intercalation into a (a) plate, (b) cylinder, (c) sphere.

GITT and EIS, despite different techniques, measure the same material property and are supposed to yield identical results. However, what has puzzled the community for a long time is that these two techniques often give an order of magnitude difference in the results.

Results

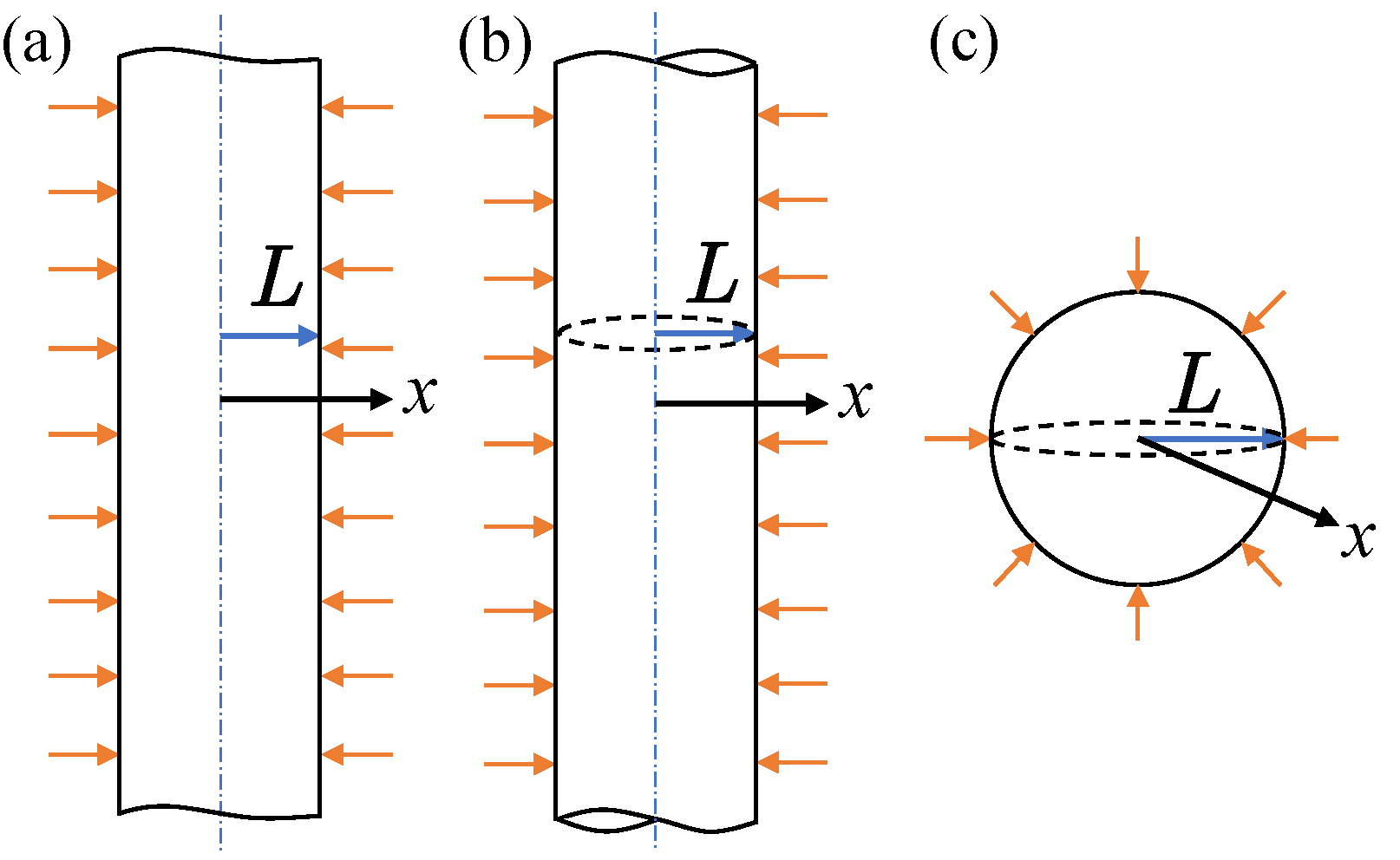
For simplicity, we assume the particle have three possible geometries (plane, cylinder, sphere).

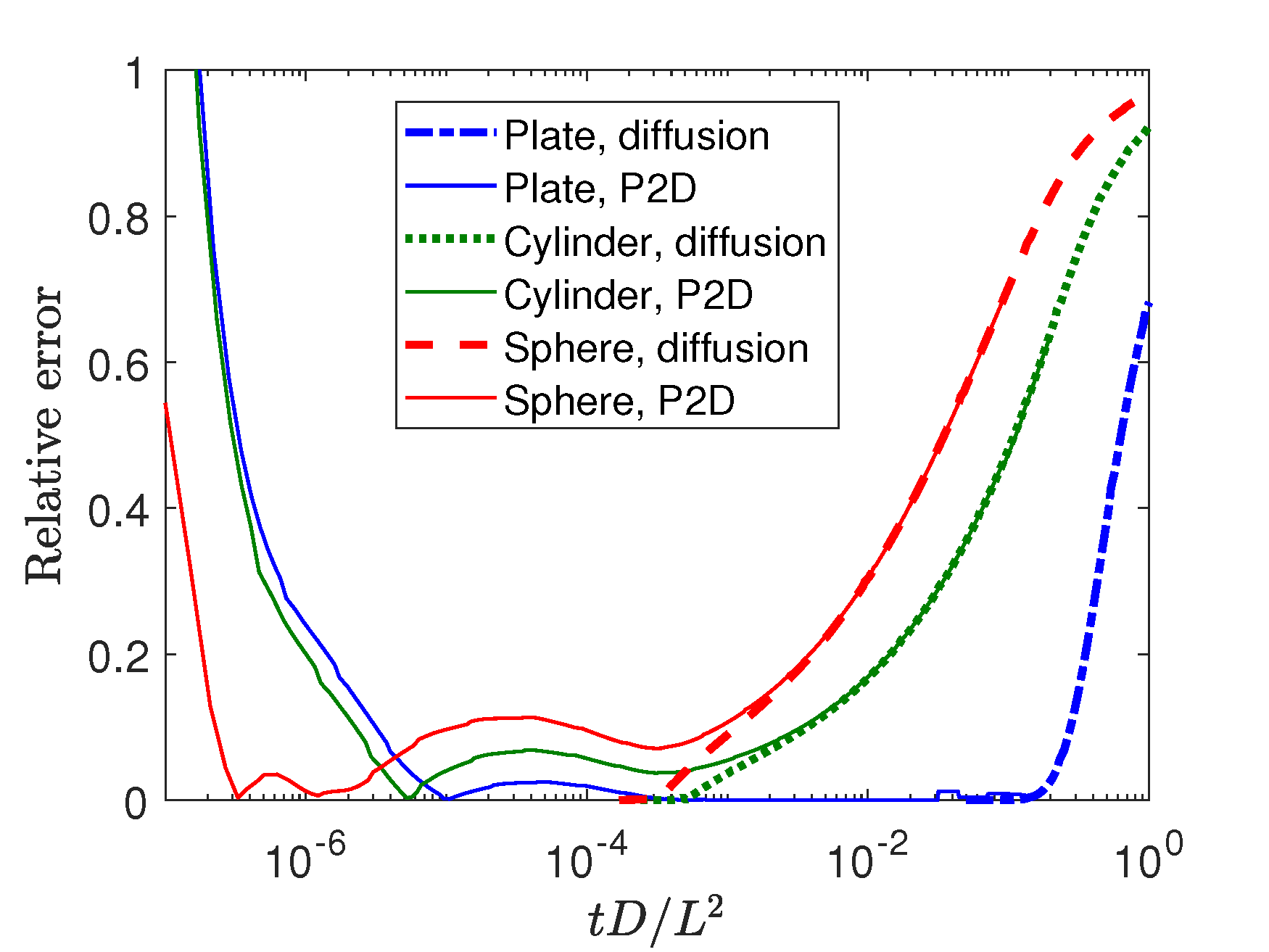
Error analysis of GITT. We use P2D model and diffusion model to study the error of Eq. (1), with respect to dimensionless time \(tD/L^2\), where \(t\) denotes time, \(D\) denotes diffusivity, \(L\) denotes half thickness (plane) or radius (cylinder and sphere). As shown in the figure below, the error of two models are almost the same after \(tD/L^2>10^{-4}\). It shows that the error mainly comes from diffusion: Eq. (1) assumes a semi-infinite plane which introduces error in practice. The error at \(tD/L^2<10^{-5}\) comes from numerical simulation, which we do not need to worry about. In experiment, transient effect may occur at this region. Overall, we need to make sure impulse time \(tD/L^2<10^{-3}\).

Relative error of diffusivity estimation by Eq (1), calculated from diffusion and P2D models. Their match shows the error comes from semi-infinite diffusion assumption of Eq. (1).

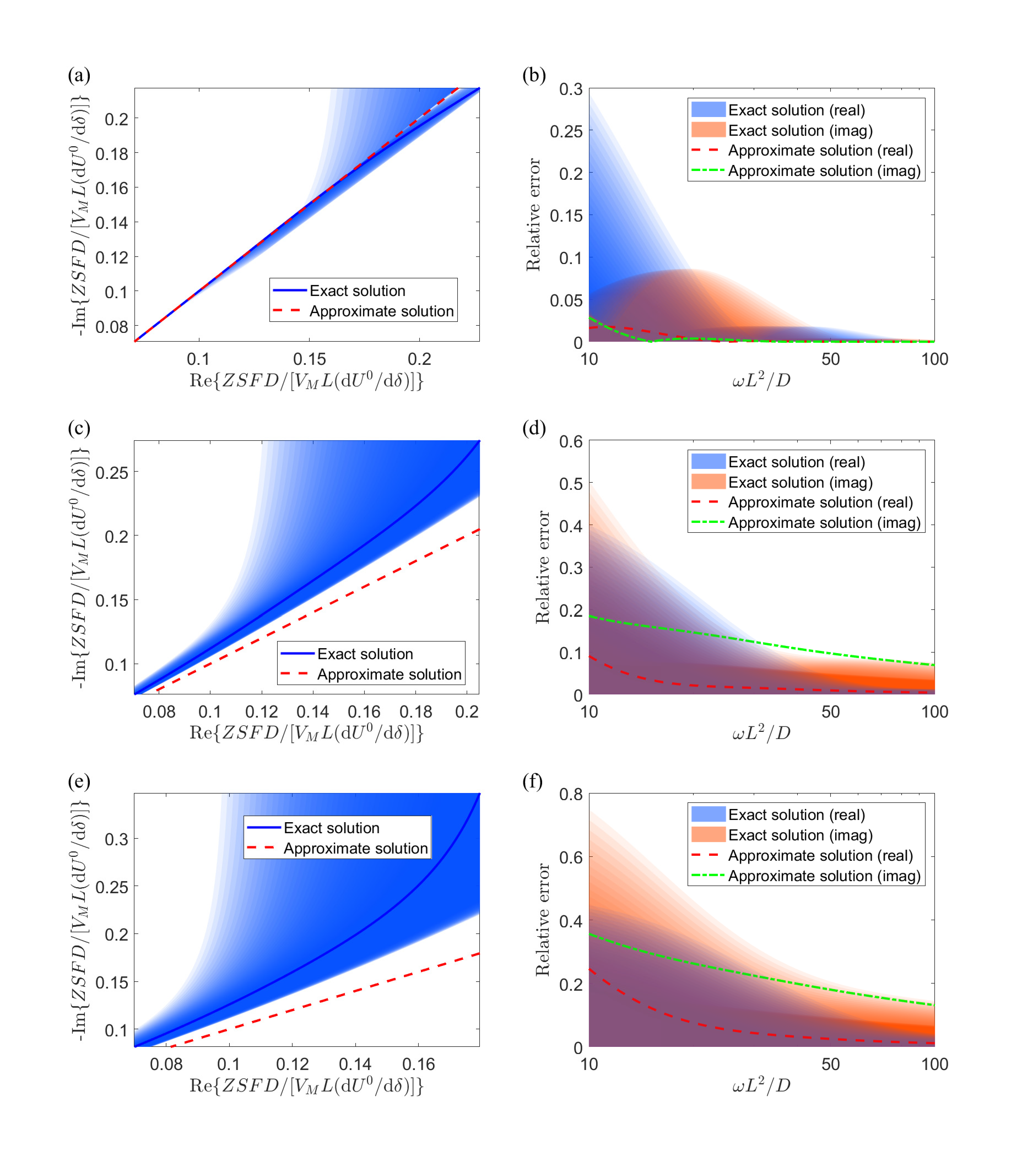
Error analysis of EIS. In EIS, what we obtain is the impedence \(Z\) with respect to current frequency \(\omega\). For three gemoetries (plane, cylinder, sphere), there exist exact solutions to obtain the diffusivity from the spectrum. A traditional way is to assume spherical particles. However, the figure below shows that the error would be huge if particle size is variant, let alone different geometries. Thus we propose to use the real part of impedence,

\[D=\frac{1}{2}\left(\frac{\mathrm{d\ }U^0}{\mathrm{d\ }\delta}\frac{V_M}{SF}\right)^2\left(\frac{\mathrm{d\ Re}\left(Z\right)}{\mathrm{d\ }\sqrt{1/\omega}}\right)^{-2}, \qquad (2)\]

which is independent of either particle size or geometry. The figure below shows our approach forms a curve (since it is independent of particle size) and has a lower error than using exact solutions (which is dependent on particle size and forms a band). Althouth our method reduces error, we still need \(\omega L^2/D>80\).

Assuming particle size a random variable, results for particle shape of (a, b) plate, (c, d) cylinder, (e, f) sphere. Left column: impedance from the exact solutions (appears as a band because of particle size distribution) and from the approximate solution of Eq. (2) (appears as a curve because of independence on particle size). The shade reflects probability, with darker for higher probability. Right column: relative error of diffusivity estimation for distributed particle sizes. The shade reflects probability.

Experimental verification. In the error analysis, we show that the time of current impulse for GITT should be short (\(t\ll L^2/D\)) and the frequency of EIS should be high (\(\omega \gg D / L^2\)). If the conditions are met, we can get almost identical results from these two methods, as shown in the figure below.

Diffusivity from EIS vs. GITT. The values are identical along the dash line.

Conclusion

This work aims to explain the discrepancy of diffusivity measured by GITT and EIS. Quantatively, we show that the time of current impulse for GITT should be short (\(t\ll L^2/D\)) and the frequency of EIS should be high (\(\omega \gg D / L^2\)). This means, qualitively, the current excitation should only penetrate the surface of particles, otherwise the geometry would have an negative impact on measurement accuracy.

  1. Consistent diffusivity measurement between Galvanostatic Intermittent Titration Technique and Electrochemical Impedance Spectroscopy
    Changyu Deng, and Wei Lu
    Journal of Power Sources 2020
    Abs HTML PDF